ക്വാണ്ടം മെക്കാനിക്സും സംഗീതവും തമ്മിലെന്ത്?

ക്വാണ്ടം മെക്കാനിക്സിന്റെയും (Quantum Mechanics) സംഗീതത്തിന്റെയും ലോകങ്ങൾ തമ്മിൽ, പ്രത്യേകിച്ച്, താളവും പാറ്റേണുകളും സംബന്ധിച്ചിടത്തോളം, കൗതുകകരമായ സാമ്യങ്ങൾ കാണാം. ഇവയുടെ ബന്ധം നേരിയതായ ഭൗതിക ബന്ധങ്ങളിലുപരി ആശയപരവുമായും ഗണിതശാസ്ത്രപരവുമായും ആഴമുള്ളതാണെന്നും ഇവയിൽ നിന്നുള്ള നിരീക്ഷണങ്ങൾ ഇരു മേഖലകളുടെയും സ്വഭാവത്തെക്കുറിച്ച് പുതിയ ഉൾക്കാഴ്ചകൾ നല്കുന്നവയാണെന്നും പറയാൻ കഴിയും.

1. താളപരമായ പാറ്റേണുകളും ഫ്രാക്റ്റലുകളും

പ്രകൃതിയിലും ക്വാണ്ടം സിസ്റ്റങ്ങളിലും കാണപ്പെടുന്ന സ്വയം ആവർത്തന പാറ്റേണുകളായ ഫ്രാക്റ്റലുകൾ (Fractals) സംഗീതത്തിലും പ്രത്യക്ഷപ്പെടുന്നു. സംഗീതത്തിലെ താളചുരുളുകൾ പലപ്പോഴും വിവിധ സ്കെയിലുകളിൽ ആവർത്തിക്കപ്പെടുന്ന ഘടനകളായതിനാൽ ഫ്രാക്റ്റൽ സ്വഭാവം പ്രകടിപ്പിക്കുന്നു. ഈ സ്വയംസമാനത (self-similarity) സംഗീതത്തെ കൂടുതൽ ആകർഷകവും സങ്കീർണ്ണവുമാക്കുന്നു.

ക്വാണ്ടം മെക്കാനിക്സിലും ഇത്തരം പാറ്റേണുകൾ കണ്ടുവരുന്നു- ഉദാഹരണത്തിന്, ഊർജ്ജ നിലകളുടെ വിഭജനം, കണികകളുടെയും തരംഗങ്ങളുടെയും സ്വഭാവം എന്നിവയിൽ. ഈ ഫ്രാക്റ്റൽ ഘടനകൾ വിശകലനം ചെയ്യാൻ ഉപയോഗിക്കുന്ന ഗണിതസിദ്ധാന്തങ്ങൾ സംഗീതത്തിന്റെ പാറ്റേണുകളും വിശദമാക്കാൻ സഹായകമാണ്.

2. എൻറാങ്കിൾമെൻ്റും (Entanglements) സാമഞ്ജസ്യവും (Symphony)

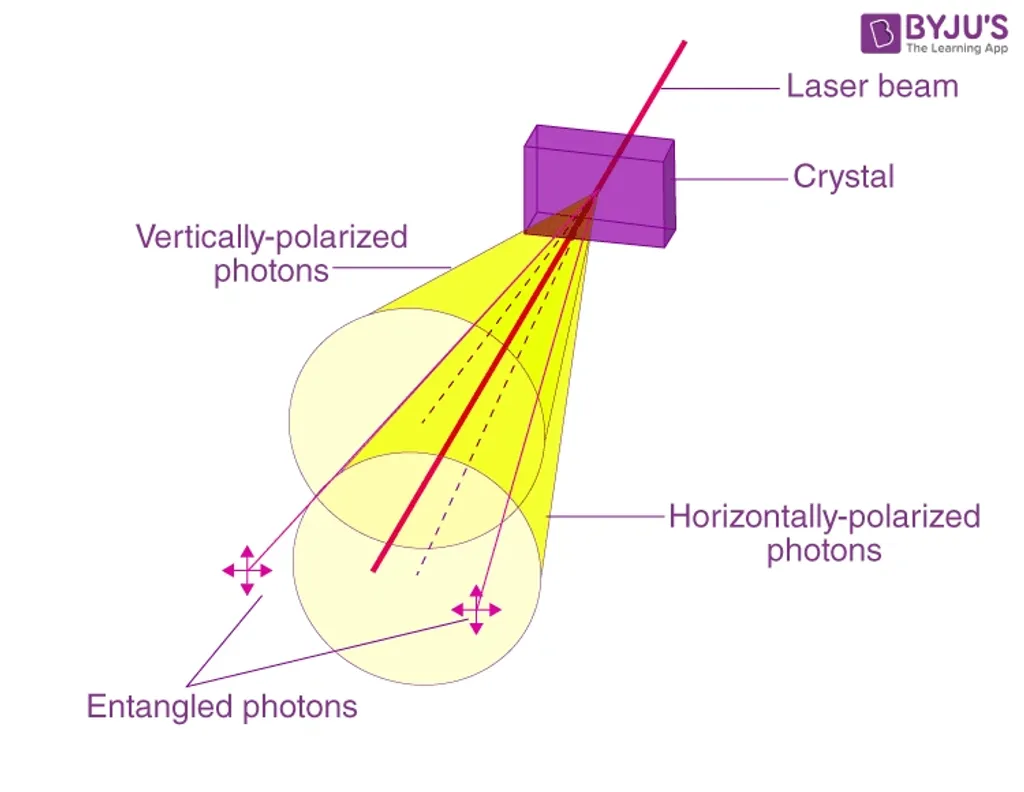
ക്വാണ്ടം മെക്കാനിക്സിലെ ഏറ്റവും അത്ഭുതകരമായ പ്രതിഭാസങ്ങളിൽ ഒന്നാണ് എൻറാങ്കിൾമെന്റ്, ഒരേ സമയം വ്യത്യസ്ത സ്ഥിതികളിലുള്ള കണികകൾ പരസ്പരം ബന്ധപ്പെട്ടു നിലനിൽക്കുന്നു എന്നത്. ഈ സ്ഥിതിയെ സംഗീത സാമഞ്ജസ്യവുമായി, വിവിധ സ്വരങ്ങൾ അല്ലെങ്കിൽ ഉപകരണങ്ങൾ ചേർന്ന് ഏകോപിതമായ നാദം സൃഷ്ടിക്കുന്നതുമായി താരതമ്യപ്പെടുത്താം.

സാമഞ്ജസ്യവും അനുരണനവും (harmony and resonance) സംഗീതത്തിലെ കേന്ദ്രീയ തത്വങ്ങളാണ്. വ്യത്യസ്ത തരത്തിലുള്ള ക്വാണ്ടം അവസ്ഥകളും താളഘടനകളും അനുരണനത്തിലൂടെ ഏകീകരിക്കപ്പെടുന്നതിനെ പോലെ, സംഗീതത്തിലെ കോർഡുകളും താളങ്ങളുമാണ് ഏകതയുടെ (unity) ആധാരങ്ങൾ.

3. ക്വാണ്ടം കമ്പ്യൂട്ടിംഗും സംഗീതസംവിധാനവും

അൽഗോരിതമിക് രചന വഴി സംഗീതം സൃഷ്ടിക്കാൻ ക്വാണ്ടം കമ്പ്യൂട്ടിങ്ങ് ശക്തമായ ഉപാധിയാകുന്നുണ്ട്. ക്ലാസിക്കൽ കമ്പ്യൂട്ടറുകൾക്ക് കൃത്യമായി മോഡലാക്കാനാകാത്ത സമന്വയഘടനകളും ക്വാണ്ടം അൽഗോരിതങ്ങൾ ഉപയോഗിച്ച് സാദ്ധ്യമാക്കാൻ കഴിയും. ഇതുവഴി ക്വാണ്ടം തത്വങ്ങൾ സംഗീത സൃഷ്ടിക്കുള്ള അനന്ത സാധ്യതകളിലേക്ക് വഴി തുറക്കുന്നു.

ക്വാണ്ടം ക്രമരഹിതത്വം (quantum randomness) പ്രവചനാതീതമായ സംഗീതാഭിപ്രായങ്ങൾക്ക് ചിറകേകുന്നു. ഈ അനിശ്ചിതത്വം ഉപയോഗിച്ച് അതീവ പുതുമയുള്ള അവിശ്വാസ്യനീയമെന്നു തോന്നാവുന്ന സംഗീതരൂപങ്ങൾ സൃഷ്ടിക്കപ്പെടുന്നു. സങ്കീർണ്ണതയും ലാളിത്യവുമെല്ലാം കലാപരമായ സൃഷ്ടികളിലേക്ക് കേന്ദ്രീകരിക്കുന്നു.

4. ഗണിതശാസ്ത്രപരമായ സമാന്തരങ്ങൾ

സംഗീത സിദ്ധാന്തത്തിന്റെയും ക്വാണ്ടം ഭൗതികശാസ്ത്രത്തിന്റെയും അടിത്തറയിൽ ഗണിതശാസ്ത്രം ആഴത്തിൽ വ്യാപിച്ചിരിക്കുന്നു. പ്രത്യേകിച്ച് ഗ്രൂപ്പ് തിയറി (Group Theory) പോലുള്ള സിദ്ധാന്തങ്ങൾ ഇരു മേഖലകളിലും പ്രധാനമാണ്. സംഗീതത്തിലെ താളഘടനകളും സാമഞ്ജസ്യ ഘടനകളും വിശകലനം ചെയ്യുന്നതിന് ഈ സിദ്ധാന്തങ്ങൾ പ്രയോജനപ്പെടുന്നു; അതുപോലെ ക്വാണ്ടം സിസ്റ്റങ്ങളിലെ കണികകളുടെയും അവയുടെ ബലങ്ങളുടെയും സ്വഭാവം വിശകലനം ചെയ്യാനും ഇതുപയോഗിക്കുന്നു.

തരംഗങ്ങളുടെയും സൂപ്പർപോസിഷൻ തത്വങ്ങളുടെയും (superposition) ഉപയോഗം ഇരു മേഖലകളിലും അടിസ്ഥാനപരമാണ് — ശബ്ദ തരംഗങ്ങൾ സംഗീതത്തിൽ പരസ്പരം ലയിച്ച് പുതുമയുള്ള പാറ്റേണുകൾ സൃഷ്ടിക്കുന്നതുപോലെ, ക്വാണ്ടം നിലകളുടെ സംയോജനവും അതേപോലെ പ്രവർത്തിക്കുന്നതായി കരുതാവുന്നതാണ് .

ഈ സമാന്തരങ്ങൾ കാണിക്കുന്നത് ക്വാണ്ടം മെക്കാനിക്സിന്റെയും സംഗീതത്തിന്റെയും അടിസ്ഥാനപരമായ ഘടനകൾ തമ്മിലുള്ള ഗണിതശാസ്ത്രപരമായ, ആശയപരമായ ബന്ധങ്ങളാണ്. വ്യത്യസ്ത മേഖലയിലുള്ള അറിവുകൾ തമ്മിൽ ഇങ്ങനെ കൂട്ടിച്ചേർക്കുമ്പോൾ, സർഗാത്മവുമായ സൃഷ്ടിപരവുമായ പുതിയ വഴികൾ സംഗീതത്തിലും ശാസ്ത്രത്തിലും തുറന്നുകൊടുക്കപ്പെടുന്നു.

▮

(കുറിപ്പ്: പരമ്പരാഗത വാദ്യോപകരണങ്ങൾ ഉപയോഗിച്ച് സംഗീതം അഭ്യാസിക്കുന്ന ഒരു അമച്വർ തബലിസ്റ്റെന്നനിലയിലാണ് ഈ കുറിപ്പ് എഴുതുന്നത്. ക്വാണ്ടം മെക്കാനിക്സിന്റെ സങ്കീർണ്ണതകളിലേക്കും സംഗീതവുമായുള്ള അതിന്റെ അത്ഭുതകരമായ ബന്ധങ്ങളിലേക്കും കടന്നുചെന്നത് എനിക്ക് ശരിക്കും ഒരു വെളിപാടായിരുന്നു. ഡ്രം മെഷീനുകൾ, സിന്തസൈസറുകൾ, വെർച്വൽ ഇൻസ്ട്രുമെൻ്റുകൾ, ബീറ്റ്- മേക്കിംഗ് സോഫ്റ്റ്‌വെയർ, സാമ്പിൾ പാക്കുകൾ (Drum Machines, Synthesizers, Virtual Instruments, Beat-Making Software, Sample Packs) തുടങ്ങിയ ആധുനിക സംഗീത സാങ്കേതികവിദ്യകൾ എത്രമാത്രം വിപ്ലവാത്മകമാണെന്നും, അവ പലപ്പോഴും ഈ ക്വാണ്ടം തത്വങ്ങളെ എങ്ങനെ ഉൾക്കൊള്ളുന്നുവെന്നും അവയുടെ സാധ്യതകൾ എത്ര വിപുലമാണെന്നും മനസ്സിലാക്കാൻ കഴിഞ്ഞു. ഈ വിഷയം കൂടുതൽ മനസ്സിലാക്കാൻ ശ്രമിക്കുന്ന ഒരു സംഗീത ശാസ്ത്രവിദ്യാർത്ഥിയുടെ അന്വേഷണാത്മക ആശയങ്ങളാണ് ഇവിടെ നൽകിയിരിക്കുന്നതെന്ന് സൂചിപ്പിക്കട്ടെ).