സത്താവാദവിരുദ്ധമായ ഭൗതികശാസ്ത്രത്തിനു വേണ്ടി

അതീതത്തെ കുറിച്ചു പറയാതെ, ദൈവത്തെ കുറിച്ചു പറയാതെ ഡല്യൂസ് ജീവിതത്തിന്റെ അന്തർലീനതയെ കുറിച്ചു പറയുന്നു

പ്രശസ്ത തത്ത്വചിന്തകനായ ഡല്യൂസിന്റെ ആധുനികശാസ്ത്രത്തെ കുറിച്ചുള്ള ചിന്തകളെ സംഗ്രഹിക്കാനാണ് ഈ ലേഖനത്തിലൂടെ ശ്രമിക്കുന്നത്. ഡല്യൂസ് (Deleuze) ഒരു റിയലിസ്റ്റാണ്. യഥാതഥവാദിയായ തത്ത്വചിന്തകൻ. നമ്മുടെ നിത്യപരിചയത്തിൽ വരുന്ന വസ്തുക്കളോടൊപ്പം സൈദ്ധാന്തികമായി നിർമ്മിക്കപ്പെട്ട വസ്തുക്കൾക്കും - ഉദാഹരണത്തിന്, ഇലക്‌ട്രോണുകളും പ്രോട്ടോണുകളും - യഥാർത്ഥമായ അസ്തിത്വമുണ്ടെന്നു ഡല്യൂസ് കരുതുന്നു. ഇവയ്‌ക്കെല്ലാം മനുഷ്യമനസ്സിൽ നിന്നും സ്വതന്ത്രമായ അസ്തിത്വമുണ്ട്. ഡല്യൂസ് ഭൗതികവാദപരമായ അതിഭൗതികവാദത്തെ സ്വീകരിക്കുന്നു. ഈ ചിന്തകന്റെ പരിഗണനയിൽ വരുന്ന വസ്തുക്കൾ ദ്രവ്യവുമായോ ഊർജ്ജവുമായോ ബന്ധങ്ങളില്ലാതെ അസ്തിത്വം അസാധ്യമായവയാണ്. ഡല്യൂസിന് അവയാണ് യഥാർത്ഥം.

സ്വയം സിദ്ധപ്രമാണങ്ങളെ സ്വീകരിക്കുകയും ഗണിതശാസ്ത്രത്തെ വിചിന്തനശാസ്ത്രത്തിലേക്ക് ചുരുക്കിയെടുക്കുകയും ചെയ്യുന്ന പ്രവണതകൾ സത്താവാദപരമാണ്. സത്താവാദപര(Essentialist)മായ സങ്കൽപ്പനങ്ങളോട് ഡല്യൂസ് യോജിക്കുന്നില്ല. ഒരു വസ്തു അനിവാര്യമായ ചില സത്തകൾ കൊണ്ട് നിർവ്വചിക്കപ്പെടുന്നതാണെന്ന് ഡല്യൂസ് കരുതുന്നില്ല. അതീതമായവയിൽ ഊന്നാതെ, യാഥാർത്ഥ്യത്തെ വിശദീകരിക്കാനാണ് ഡല്യൂസ് ശ്രമിക്കുന്നത്. അതീതത്തോടു ഭവശാസ്ത്രപരമായ പ്രതിജ്ഞാബദ്ധത പുലർത്താത്ത ഗണങ്ങൾ കൊണ്ട് അനിവാര്യമൂലകങ്ങളെ മാറ്റിത്തീർക്കണം. ചരിത്രവൽക്കരണത്തിലൂടെ സങ്കൽപ്പനങ്ങളിലെ അതീതസ്വഭാവത്തെ ഇല്ലാതാക്കാൻ കഴിയും. ഊർജ്ജവും ദ്രവ്യവും അന്തർലീനമായിരിക്കുന്ന ഭൗതിക, ചലനപ്രക്രിയകളിലൂടെയും ഇതു സാധ്യമാകും. സത്താപരമായ ചിന്തകളിൽ നിന്നും വിമോചിതമാകാനുള്ള ശ്രമത്തിൽ, ഗണിതശാസ്ത്രത്തിലെ അവകലനം, ഗ്രൂപ്പു സിദ്ധാന്തം, പുതിയ ജ്യാമിതികൾ ഇവയെല്ലാം നമുക്കു സഹായകമാകുന്നതാണ്.

അതീതസങ്കൽപ്പനങ്ങളെ സ്വീകരിക്കാത്ത യഥാതഥവാദം ഗണിതശാസ്ത്രം കൊണ്ട് എങ്ങനെ പ്രവർത്തിക്കുമെന്നറിയാൻ ഭൗതികശാസ്ത്രത്തിൽ അവകലനസമീകരണങ്ങൾ (Differential Equations) ഉപയോഗിക്കുന്ന രീതി മനസ്സിലാക്കിയാൽ മതിയാകും. ഏതെല്ലാം ഭൗതികരാശികളേയും ഘടകങ്ങളേയും ആശ്രയിച്ചാണ് ഒരു ഭൗതികവ്യവസ്ഥ പരിണാമത്തിനു വിധേയമാകുന്നതെന്നു ഗ്രഹിച്ചു കൊണ്ടു മാത്രമേ അതിന്റെ ഗണിതശാസ്ത്രമാതൃക നിർമ്മിക്കാനാവൂ. ഭൗതികവ്യവസ്ഥയുടെ മാതൃക അതിനു നിലനിൽക്കാൻ കഴിയുന്ന എല്ലാ അവസ്ഥകളേയും ഉൾക്കൊള്ളുന്നതായിരിക്കണം. ഈ സാധ്യതകളുടെ ഇടങ്ങളെ അവസ്ഥാസ്ഥലങ്ങളെ (State Space)ന്നു വിളിക്കാം. ഭൗതികവ്യവസ്ഥ സമയക്രമത്തിനനുസരിച്ച് മാറ്റത്തിനു വിധേയമാകുമ്പോൾ വ്യത്യസ്ത അവസ്ഥകൾ തുടർച്ചയുള്ള ബിന്ദുക്കളായി, വളഞ്ഞ രേഖകളായി, സഞ്ചാരപഥങ്ങളായി അവസ്ഥാസ്ഥലങ്ങളിൽ രേഖപ്പെടുന്നു. വ്യത്യസ്തങ്ങളായ സഞ്ചാരപഥങ്ങളുടെ ഗണം വ്യവസ്ഥയുടെ വ്യത്യസ്ത ചരിത്രങ്ങളെ ഉൾക്കൊള്ളുന്നുണ്ടെന്നു പറയാം. അവസ്ഥാസ്ഥലത്തെ ഓരോ ബിന്ദുവും വ്യത്യസ്തമായ സംഭാവ്യതകളുള്ളവയാണ്. ഭൗതികവ്യവസ്ഥ നിരന്തരം മാറിക്കൊണ്ടിരിക്കുന്നു. മാറ്റത്തിനനുസരിച്ച് അവസ്ഥാസ്ഥലത്തെ സഞ്ചാരപഥങ്ങളും മാറുന്നു, അവ അലഞ്ഞുതിരിയുന്നു. വ്യവസ്ഥയുടെ ആദ്യാവസ്ഥകൾ എന്തുമായിക്കൊള്ളട്ടെ, ദീർഘകാലം കൊണ്ട് അവയുടെ സംഭാവ്യതാചരിത്രങ്ങൾ ഒരു ഏകമാത്രബിന്ദുവിലേക്ക് എത്തിച്ചേരുന്നു. വിവിധ ഭൗതികവ്യവസ്ഥകളുടെ ഈ ഏകമാത്രബിന്ദുക്കൾ സാർവ്വലൗകികമാണെന്നത് അത്ഭുതജനകമായ സവിശേഷതയാണ്. ക്ലാസിക്കൽ ഭൗതികത്തിന്റെ എല്ലാ ശാഖകളുടേയും ഏകീകരണം പത്തൊമ്പതാം നൂറ്റാണ്ടിൽ തന്നെ ഈ സാർവ്വലൗകികസ്വഭാവം കൊണ്ട് സാധ്യമാകുമായിരുന്നു. ഈ ഗണിതവൽക്കരണത്തിലൂടെ ഭാഷോന്മുഖമായിരുന്ന ശാസ്ത്രത്തിന്റെ തത്ത്വചിന്ത അതിൽ നിന്നും മുക്തമാകുകയാണ്. സിദ്ധാന്തങ്ങളുടെ ഘടനയെ നിശ്ചയിക്കുന്ന കാര്യത്തിൽ ഭാഷ ഇടപെടുന്നില്ല. ഭാഷയേയും വിചിന്തനശാസ്ത്രത്തേയും മാറ്റി നിർത്തുകയും ഗണിതത്തിലെ അവകലനസമീകരണങ്ങൾ ഉപയോഗിച്ച് കാര്യങ്ങൾ നിർവ്വഹിക്കുകയും ചെയ്യുന്നു.

ഒരു ഭൗതികവ്യവസ്ഥയിൽ നടത്തുന്ന പരീക്ഷണങ്ങളിലൂടെ അവസ്ഥാസ്ഥലങ്ങളിലെ രേഖകൾ വരയ്ക്കുന്നതാണ് ആദ്യപടി. തുടർന്ന്, ഗണിതശാസ്ത്രമാതൃകയുടെ അടിസ്ഥാനത്തിൽ അവസ്ഥാസ്ഥലങ്ങളിലെ സഞ്ചാരപഥങ്ങൾ വരയ്ക്കുക. പരീക്ഷണശാലയിൽ ഉപയോഗിച്ച ആദ്യാവസ്ഥകൾ (Initial Conditions) തന്നെ ഗണിതശാസ്ത്രമാതൃകയ്ക്കും നൽകണം. വരച്ചു കിട്ടിയ രണ്ടു സഞ്ചാരപഥങ്ങളും ജ്യാമിതീയമായ സാദൃശ്യങ്ങൾ കാണിക്കുന്നുവെങ്കിൽ മാതൃക ശരിയായി പ്രവർത്തിക്കുന്നുവെന്നാണർത്ഥം. ഇപ്പോൾ, വ്യവസ്ഥയുടെ കമ്പ്യൂട്ടർ പ്രോഗ്രാമുകൾ നിർമ്മിക്കാനും അവയെ സിമുലേഷനുകളായി പ്രവർത്തിപ്പിക്കാനും കഴിയുന്നുണ്ട്. ഗണിതശാസ്ത്രമാതൃകകൾക്ക് സഞ്ചാരപഥങ്ങളെ സൃഷ്ടിക്കാനുള്ള ശേഷിയുണ്ട്. ഒരു വ്യവസ്ഥയെ മനസ്സിലാക്കുമ്പോൾ നമ്മുടെ കാഴ്ചയിൽ വരാത്ത സാഹചര്യങ്ങളിൽ അവ എങ്ങനെയാണെന്നു കൂടി അറിയണം.

വ്യവസ്ഥാസ്ഥലങ്ങളിലെ ബിന്ദുക്കളെ നിശ്ചയിക്കുന്ന സാധ്യതകൾ നമ്മുടെ മനസ്സുകളിൽ നിന്നും സ്വതന്ത്രമാണെന്ന് ഡല്യൂസ് കരുതുന്നില്ല. വ്യവസ്ഥാസ്ഥലങ്ങളുടെ ഘടന മാത്രമാണ് യാഥാർത്ഥ്യസംബന്ധിയായിട്ടുള്ളത്. മാതൃകകളിലെ ക്രമങ്ങളെയും ആയിത്തീരലിന്റെ അന്തർലീനമായ രീതികളെയും കുറിച്ചറിയാൻ ഡല്യൂസ് അയഥാർത്ഥ യാഥാർത്ഥ്യ(virtuality)ത്തെ കുറിച്ചു പറയുന്നു. അയഥാർത്ഥ യാഥാർത്ഥ്യം, യഥാർത്ഥ (real)മാണ്, സാക്ഷാത്ക്കൃത(actual)മല്ല.

ഡല്യൂസിന്റെ ശാസ്ത്രദർശനത്തെ കുറിച്ച് മാനുവൽ ദെളന്ദ നടത്തുന്ന വായനകൾ സവിശേഷമായ ഉൾക്കാഴ്ചകൾ നൽകുന്നതാണ്. ഡല്യൂസിന്റെ യഥാതഥഭവശാസ്ത്രം മൂന്നു വ്യത്യസ്ത മാനങ്ങളിലുള്ളതാണെന്ന് ദെളെന്ദ പറയുന്നു. അയഥാർത്ഥയഥാർത്ഥം (virtual), തീവ്രം (intensive), സാക്ഷാത്ക്കൃതം (actual) എന്നിവയാണവ. രാജകീയശാസ്ത്രം (Royal Science - സ്വയംസിദ്ധപ്രമാണങ്ങളിൽ ആരംഭിക്കുന്ന ഗണിതശാസ്ത്രത്തെ രാജകീയശാസ്ത്രത്തിന് ഉദാഹരണമായി കാണാം.) നഷ്ടപ്പെടുത്തുകയോ ഉപേക്ഷിക്കുകയോ ചെയ്യുന്നതിനെ തീവ്രശാസ്ത്രം (Intensive Science) തിരിച്ചെടുക്കുന്നു. ഡല്യൂസിന്റെ ബഹുലതകളെ കുറിച്ചുള്ള സിദ്ധാന്തത്തിന്റെ ഭാഗമായ വ്യവകലിതനാനാത്വ (differential manifolds)ങ്ങളെ കുറിച്ചുള്ള ഔപചാരിക സങ്കൽപ്പനങ്ങൾ ദെളെന്ദയുടെ പുനർനിർമ്മാണത്തിലൂടെ കൂടുതൽ തെളിമയുള്ളതായി. ദെളന്ദ രൂപപ്പെടുത്തിയ ബഹുലതകളുടെ സിദ്ധാന്തം യഥാതഥവാദത്തിന്റെ ഭവശാസ്ത്രത്തെ നന്നായി പ്രകാശിപ്പിക്കുന്നുണ്ടായിരുന്നു.

ദെളന്ദ നിർവ്വഹിച്ച പുനർനിർമ്മാണത്തിൽ തത്ത്വചിന്തയിലെ ഗണിതശാസ്ത്രവസ്തുക്കൾ യഥാർത്ഥമായതിന്റെ ശരിപകർപ്പുകളല്ല, ക്രമരഹിതമായ ചിന്തയുടെയും ഭാവനയുടേയും അമൂർത്ത സൃഷ്ടികളുമല്ല. ദെളന്ദയുടെ മാതൃകകളായി വരുന്ന വസ്തുക്കൾ അനശ്വരസത്തകളോ ഘടനകളോ ഉള്ളവയല്ലെന്നു സ്ഥാപിക്കാൻ അദ്ദേഹം ശ്രമിക്കുന്നുണ്ട്. മാതൃകവൽക്കരണത്തിനു സ്വീകരിക്കപ്പെടുന്ന പ്രമാണങ്ങളിലൂടെ അവ സത്തകൾക്കു കീഴ്‌പ്പെടുന്നില്ല.

ഡല്യൂസിന്റെ ഭവശാസ്ത്രത്തിൽ ബഹുലത എന്ന സംപ്രത്യയം വളരെ പ്രധാനമാണ്. വ്യവകലിതനാനാത്വങ്ങളെ കുറിച്ചുള്ള ഗൗസിന്റേയും റീമാന്റേയും ഗണിതശാസ്ത്രസിദ്ധാന്തങ്ങളിൽ നിന്നും ഡല്യൂസിന്റെ ബഹുലത എന്ന സംപ്രത്യയത്തെ കണ്ടെത്താം. വ്യവസ്ഥകളുടെ ആന്തരികമായ പരിവർത്തനങ്ങളെ കാണിക്കുന്ന ഭൗതികയാഥാർത്ഥ്യവൽക്കരണങ്ങളുടെ ബഹുലരൂപങ്ങളെന്ന നിലയ്ക്ക് ബഹുലതകളെ ഗ്രഹിക്കുന്നതിനെയാണ് ഇവിടെ ഉദ്ദേശിക്കുന്നത്. നിഗൂഢതലങ്ങളെ നിർവ്വചിക്കുന്ന ആകർഷക (attractor)ങ്ങളും സമമിതി തകരുന്ന വ്യതിചലന (bifurcation)ങ്ങളും മറ്റുമായി പരസ്പരം ബന്ധപ്പെടുന്ന കൂടിക്കുഴഞ്ഞ സദിശബലക്ഷേത്ര (vector field)ങ്ങളുടെ ഗണമാണ് ബഹുലതയെന്ന് ദെളെന്ദ ഡല്യൂസിന്റെ സംപ്രത്യയത്തെ നിർവ്വചിക്കുന്നുണ്ട്. വളവുകളും പ്രതലങ്ങളും സ്ഥലങ്ങളായി രൂപപ്പെടുന്നതിനെ കുറിച്ചാണ് ഗൗസിന്റെ വ്യവകലിതനാനാത്വങ്ങളെ കുറിച്ചുള്ള സിദ്ധാന്തം പറയുന്നത്. സ്ഥലത്തെ വളവുമായി ബന്ധിപ്പിക്കുന്ന സങ്കൽപ്പനം ഐൻസ്റ്റൈന്റെ സാമാന്യ ആപേക്ഷികസിദ്ധാന്തത്തിൽ ഉപയോഗിക്കപ്പെടുന്നുണ്ട്. ആപേക്ഷികസിദ്ധാന്തത്തിന്റെ വിശദീകരണങ്ങളിൽ ഗോളത്തിന്റെ ഉപരിതലം അതിർത്തികളില്ലാത്ത വളഞ്ഞസ്ഥലമായി, നേർപ്രതലം വളച്ചെടുത്ത് രൂപപ്പെടുത്തിയതായി സങ്കൽപ്പിക്കുന്നതു കാണാം. സ്ഥലത്തിൽ അന്തഃസ്ഥിതമായ അവകലനസമീകരണങ്ങൾ കൊണ്ട് ഈ വളഞ്ഞ പ്രതലങ്ങളെ സ്വഭാവവൽക്കരിക്കാൻ കഴിയുമെന്ന് കാൾ ഗൗസ് പറയുന്നുണ്ട്. സമാന്തരരേഖകളെ കുറിച്ചുള്ള യൂക്ലിഡിന്റെ സ്വയംസിദ്ധപ്രമാണത്തേയും തിരശ്ചീനജ്യാമിതിയേയും ഉപേക്ഷിച്ചു കൊണ്ടാണ് ഗൗസിന്റെ നിർദ്ദേശങ്ങളും റീമാനിയൻ ജ്യാമിതിയും രൂപീകരിക്കപ്പെടുന്നത്. ഗൗസിന്റെ സിദ്ധാന്തത്തിൽ തെളിയുന്ന ജ്യാമിതീയ അന്തഃസ്ഥിതത്വ (Geometrical Immanence)ത്തെ കുറിച്ചുള്ള ആശയം വളരെ പ്രധാനമാണെന്ന് ദെളന്ദ സൂചിപ്പിക്കുന്നു. വളഞ്ഞ സ്ഥലങ്ങളെ കുറിച്ചുള്ള ഈ ആശയം വ്യവഹാരസ്ഥലങ്ങളിലേക്ക് വ്യാപിപ്പിക്കാവുന്നതാണ്. ഡല്യൂസിന്റെ പദ്ധതികൾക്ക് പൂരകമാകുന്ന വിധത്തിൽ, സത്താവാദത്തിന്റെ പിടിയിൽ നിന്നും വിമുക്തമായ രൂപത്തിൽ ബഹുലതകളുടെ സിദ്ധാന്തത്തെ പുനർനിർമ്മിക്കാൻ ദെളന്ദയ്ക്കു കഴിയുന്നുണ്ട്. മിക്കവാറും സ്വയംസിദ്ധപ്രമാണങ്ങളുടെ അടിസ്ഥാനത്തിൽ നിർമ്മിക്കപ്പെടുന്ന ഗണിതശാസ്ത്രപ്രയോഗത്തിന്റെ മണ്ഡലത്തിൽ പോലും സത്താവിരുദ്ധമായ അവകാശവാദങ്ങൾ ഉന്നയിക്കാൻ കഴിയുന്ന സ്ഥിതിയാണ് സംജാതമായത്.

ഡല്യൂസിന്റെ ഭവശാസ്ത്രത്തിൽ സാക്ഷാത്ക്കൃതവസ്തുവോ പ്രതിഭാസമോ അവയുടെ യാഥാർത്ഥ്യത്തെ പൂർണ്ണമായും വെളിപ്പെടുത്തുന്നില്ല. അതിൽ സ്വത്വത്തിനെതിരെ വ്യത്യാസവും ഏകത്വത്തിനെതിരെ ബഹുലതകളും കടന്നു വരുന്നു. ശുദ്ധവ്യത്യാസമാണ് എല്ലാ വ്യത്യാസങ്ങളേയും രൂപപ്പെടുത്തുന്നതെന്ന് ഡല്യൂസ് പറയും. ശുദ്ധവ്യത്യാസത്തെയാണ് അയഥാർത്ഥയഥാർത്ഥം എന്നു വിളിക്കുന്നത്. ഈ തത്ത്വചിന്തകന്റെ ഭവശാസ്ത്രത്തിലെ ഒരു മുഖ്യസംപ്രത്യയമാണിത്. സാധ്യതകളുടെ ഒരു മണ്ഡലം മാത്രമല്ല, അത് യാഥാർത്ഥ്യത്തിന്റെ മറ്റൊരു മാനമാണ്. നാം സംവദിക്കുന്ന സാക്ഷാത്ക്കൃതലോകത്തെ രൂപീകരിക്കുന്ന വ്യത്യാസങ്ങളുടെ യഥാർത്ഥമണ്ഡലമാണത്. അയഥാർത്ഥയാഥാർത്ഥ്യത്തിന്റെ സാക്ഷാത്ക്കാരപ്രക്രിയയെയാണ് വ്യവകലനം (differentiation)എന്നു വിളിക്കുക. വ്യത്യാസത്തെ കുറിച്ചുള്ള ഈ സർഗപരമായ ഭവശാസ്ത്രത്തിന്റെ രൂപീകരണത്തിൽ ശാസ്ത്രത്തിനു വലിയ പങ്കുണ്ട്.

വ്യവസ്ഥാസ്ഥലത്തിന്റെ പരോക്ഷഘടന മാത്രമേ മനസ്സിൽ നിന്നും സ്വതന്ത്രമായി നിൽക്കുന്നതായി ഡല്യൂസ് പരിഗണിക്കുന്നുള്ളൂ. വ്യവസ്ഥാസ്ഥലങ്ങൾ യൂക്ലീഡിയൻ സ്ഥലങ്ങളല്ല. അവ തീവ്രവേഗങ്ങളുടേയും മന്ദഗതിയുടേയുമെല്ലാം സദിശങ്ങൾ കൂടിയാണ്. വ്യവസ്ഥാസ്ഥലത്തിന്റെ പ്രവേഗദിശാക്ഷേത്ര (Velocity Vector Field)ത്തെ കുറിച്ചു പറയേണ്ട സന്ദർഭമാണിത്. സഞ്ചാരപഥങ്ങൾ ആകർഷണകേന്ദ്രങ്ങളിലേക്കു നീങ്ങിക്കൊണ്ടിരിക്കുകയാണ്, അവ ആകർഷകങ്ങളിൽ എത്തിച്ചേരുന്നില്ല, അത് അനന്തം അകലെയാണ്. ഒരു ആകർഷണകേന്ദ്രത്തിന്റെ സ്വാധീനപരിധികൾ അവസ്ഥാസ്ഥലത്തിലുള്ള ബിന്ദുക്കളുടെ ഒരു ഉപഗണമാണ്. അവയും സാധ്യമായ അവസ്ഥകളെ സൂചിപ്പിക്കുന്നവയാണ്. എന്നാൽ, ആകർഷണകേന്ദ്രം ഒരു സാധ്യതാബിന്ദുവല്ല. എന്തുകൊണ്ടെന്നാൽ, അത് ഒരിക്കലും സാക്ഷാത്കൃതമാകുന്നില്ല. ആകർഷണകേന്ദ്രങ്ങളെ ഒരിക്കലും സാക്ഷാൽക്കരിക്കാൻ കഴിയില്ല. സഞ്ചാരപഥങ്ങൾ ഒരിക്കലും ആകർഷണകേന്ദ്രങ്ങളിൽ എത്തിച്ചേരുന്നില്ല. അങ്ങനെ, ആകർഷണകേന്ദ്രങ്ങൾ സാക്ഷാത്കൃതമാകാതിരിക്കുമ്പോഴും യഥാർത്ഥമാണ്. അതാണ് സഞ്ചാരപഥങ്ങൾക്ക് ആന്തരികമായ സന്തുലിതാവസ്ഥ നൽകുന്നത്. ആകർഷകങ്ങൾ വ്യവസ്ഥയുടെ ദീർഘകാലപ്രവണതകളെയാണ് സൂചിപ്പിക്കുന്നത്. അത് സാധ്യമായ സ്ഥിതിയെ സൂചിപ്പിക്കുന്നില്ല. യാദൃച്ഛികതകൾക്കും അനിവാര്യതകൾക്കും അപ്പുറം ഒരു പുതിയ ഭൗതികസാമ്പ്രദായികക്രമത്തെ ആവശ്യപ്പെടുന്ന സന്ദർഭമാണിത്. അതിന്റെ പ്രഭാവങ്ങളിൽ യഥാർത്ഥവും എന്നാൽ ഒരിക്കലും സാക്ഷാത്കൃതവുമാകാത്ത ആകർഷകങ്ങളുടെ, ഏകമാത്രബിന്ദുക്കളുടെ ഇരട്ടപ്പദവിയെ വിശദീകരിക്കുന്നതിന് ഇത് ആവശ്യമാണ്. ഡല്യൂസ് അയഥാർത്ഥ യാഥാർത്ഥ്യ (virtuality)മെന്ന സങ്കൽപ്പനത്തിലൂടെ നേടിയെടുക്കുന്നത് അതാണ്. ഭൗതികശാസ്ത്രത്തിലെ പ്രശ്‌നങ്ങൾക്ക് അവയുടെ നിർദ്ധാരണമൂല്യങ്ങളിൽ നിന്നും സ്വതന്ത്രമായി വസ്തുനിഷ്ഠത ഉണ്ടെന്നതിന്റെ തെളിവാണിത്. ഭൗതികശാസ്ത്രത്തിലെ പ്രശ്‌നങ്ങൾക്ക് നിർദ്ധാരണമൂല്യങ്ങളിൽ നിന്നും സ്വതന്ത്രമായ സ്വേച്ഛാസ്വഭാവം ഉണ്ടെന്നതിന്റെ സൂചനയാണിത്. മാത്രമല്ല, അസ്സൽ ഗണങ്ങളോടൊപ്പം ഉപഗണങ്ങൾക്കുള്ള സാധ്യതകൾ കൂടി നിലനിൽക്കുന്നതു കൊണ്ട് പ്രശ്‌നങ്ങൾ കൂടുതൽ മെച്ചപ്പെട്ട രീതിയിൽ നിർവ്വചിക്കാൻ കഴിയുന്നു. ഡല്യൂസിനെ സംബന്ധിച്ചിടത്തോളം ഭൗതികശാസ്ത്രത്തിലെ പ്രശ്‌നങ്ങളെ രേഖപ്പെടുത്തുന്നതിന് ഗണിതശാസ്ത്രത്തിന് വ്യത്യസ്തമായ നിരവധി മാർഗങ്ങളുണ്ട്. ശാസ്ത്രത്തിന്റെ ഭാഷേതരമായ ഉള്ളടക്കത്തിന്റെ ഭാഗമാണിത്. ശാസ്ത്രത്തിന്റെ ദർശനത്തിന്നാവശ്യമായ വളരെ പ്രധാനപ്പെട്ട ഉൾക്കാഴ്ചയാണിത്. ഇതിന്റെ അനന്തരഫലങ്ങൾ ശാസ്ത്രത്തിൽ മാത്രം ഒതുങ്ങിനിൽക്കുന്നില്ല.

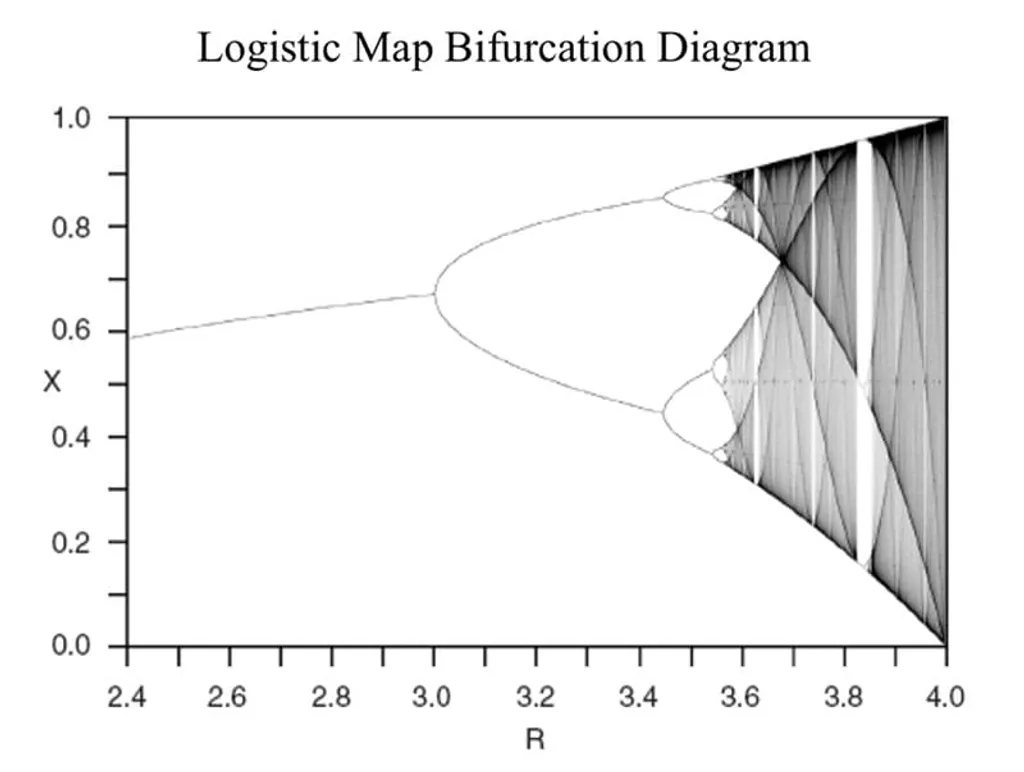
വ്യതിചലിതങ്ങൾ (Bifurcations)എന്നു വിളിക്കാവുന്ന ഗണിതശാസ്ത്രപ്രതിഭാസങ്ങളിൽ, ആകർഷകകേന്ദ്രങ്ങളുടെ വിതരണം ഒരേ രൂപത്തിലല്ല. ചിലപ്പോൾ ആകർഷകങ്ങളുടെ എണ്ണമാണ് വ്യത്യാസപ്പെടുന്നത്. ചില സന്ദർഭങ്ങളിൽ അവയുടെ പ്രകൃതമാണ് മാറുന്നത്. ബിന്ദു ആകർഷക(Point Attractors)ങ്ങൾ രേഖ ആകർഷക(Line Attractors)ങ്ങളായി മാറുന്നു. ഹോഫ് വ്യതിചലിതങ്ങൾ (Hopf bifurcations) ഇങ്ങനെയാണ് പെരുമാറുന്നത്. സമയബന്ധിതമായ ആകർഷകങ്ങൾ ക്രമരഹിത(Chaotic)മായ ആകർഷകങ്ങളായി മാറുന്നു. ഫെയ്ൻബാം വ്യതിചലിതങ്ങൾ (Feigenbaum bifurcations)ഇങ്ങനെയാണ് രൂപം കൊള്ളുന്നത്. വ്യവസ്ഥാസ്ഥലങ്ങളിലെ സദിശബലക്ഷേത്രങ്ങളിൽ നടക്കുന്ന ഗണിതശാസ്ത്രസംഭവങ്ങളാണിവ. ഗണിതശാസ്ത്രസമീകരണങ്ങളിലെ ചില ഘടകങ്ങൾക്കു വരുത്തുന്ന ചെറിയ വ്യതിയാനങ്ങൾ, ആദ്യാവസ്ഥകളിലുണ്ടാകുന്ന ചെറിയ വ്യത്യാസങ്ങൾ ഇവയെല്ലാം വലിയ വ്യതിചലനങ്ങൾക്ക് കാരണമാകുന്നു. സമമിതിയുടെ നാശം വ്യതിചലിതമായ അവസ്ഥകൾക്ക് കാരണമാകുന്നു. സ്ഥിതാവസ്ഥകൾ, കാലികമായി മാറുന്ന അവസ്ഥകൾ, ക്രമരഹിതമായ അവസ്ഥകൾ എന്നിങ്ങനെ പ്രശ്‌നങ്ങളുടെ നിർദ്ധാരണമൂല്യങ്ങൾ മാറി മാറി വരുന്നു. അവസ്ഥാസ്ഥലങ്ങളിലെ സഞ്ചാരപഥങ്ങൾ ഭൗതികവ്യവസ്ഥയുടെ അവസ്ഥകളുടെ പരിണാമത്തെ കുറിച്ചുള്ള ചിത്രം തുടർച്ചയായ അളവുകളിലൂടെ സാധ്യമാക്കുന്നതു പോലെ, തുടർച്ചയുള്ള ഗണിതശാസ്ത്രസംഭവങ്ങൾക്ക് ഭൗതികസംഭവങ്ങളെ രേഖപ്പെടുത്താൻ കഴിയുമെന്ന അടിസ്ഥാനധാരണയാണ് ഇവിടെ പ്രവർത്തനക്ഷമമാകുന്നത്. സഞ്ചാരപഥങ്ങളുടെ കാര്യത്തിൽ മാറ്റങ്ങൾ അളവുപരമായി രേഖപ്പെടുമ്പോൾ വ്യതിചലിതങ്ങളുടെ കാര്യത്തിൽ അത് ഗുണപരമായി രേഖപ്പെടുന്നു. ഗുണപരമായ പ്രക്രിയകൾ അളവുപരമായ പ്രക്രിയകളെ അപേക്ഷിച്ച് കൂടുതൽ അടിസ്ഥാനപരമാണ്. അളവുപരമായത് ഗുണപരമായതിന്റെ പ്രത്യേക അവസ്ഥകൾ മാത്രമാണ്. അളവുപരമായതിന്റേയും ഗുണപരമായതിന്റേയും ഇടയിലെ കണ്ണി ഭൗതികയാഥാർത്ഥ്യത്തിന്റെ രൂപീകരണത്തിൽ പ്രധാനമാകുന്നതായി ഡല്യൂസ് കാണുന്നു.

സാധ്യതാസ്ഥലങ്ങളിലെ പരോക്ഷഘടനകളുടെ വ്യതിചലിതമായ യഥാതഥവൽക്കരണങ്ങളെ ഡല്യൂസ് വളരെ പ്രാധാന്യത്തോടെയാണ് കണ്ടത്. പ്ലാറ്റോണിക് സത്തകളെ ഭവശാസ്ത്രത്തിലേക്ക് കൊണ്ടുവരുന്നതിന് ഡല്യൂസ് എതിരാണ്. ഗോളാകൃതിയേയും സമചതുരാകൃതിയേയും പോലുള്ള നിർണ്ണയവാദപരമായ രൂപങ്ങൾക്കു പകരം ക്രമരഹിതമായ വ്യതിചലിതങ്ങളെയാണ് ഡല്യൂസിന്റെ ചിന്ത സ്വീകരിക്കുന്നത്. അതീതസങ്കൽപ്പനങ്ങൾക്കെതിരായ സമീപനമാണിത്. പൊട്ടിപ്പിരിയുകയും വേർപിരിയുകയും കൂടിച്ചേരുകയും ഒക്കെ ചെയ്യുന്ന അവയുടെ അയഥാർത്ഥയഥാർത്ഥഘടന (Virtual Structure) തന്നെ ഡല്യൂസ് സത്തകളെ തന്റെ ഭവശാസ്ത്രത്തിലേക്കു പ്രവേശിപ്പിച്ചിട്ടില്ലെന്നതിന്റെ തെളിവാണ്. ഗോളരൂപങ്ങളോ വൃത്തങ്ങളോ പോലെ സത്തയെ ആവാഹിച്ചു കൊണ്ടുവരുന്ന ജ്യാമിതീയരൂപങ്ങൾക്കു പകരം ഫെയ്ൻബാം വ്യതിചലിതങ്ങളേയും ഹോഫ് വ്യതിചലിതങ്ങളേയും വളരെ ക്രമരഹിതമായ അവസ്ഥകളേയും ഒക്കെ സാധ്യമാക്കുന്ന രൂപങ്ങളാണ് വ്യവസ്ഥാസ്ഥലങ്ങളിൽ ദൃശ്യമാകുന്നത്. മാറ്റമില്ലായ്മയെ കുറിച്ചു നാം പറയുന്നുവെങ്കിൽ, അത് അനശ്വരമായ സത്തയെ കുറിച്ചുള്ള സൂചനകളെ ഉൾവഹിക്കുന്നതാകുമല്ലോ? സ്വയംസിദ്ധപ്രമാണങ്ങളുടെ ഉറച്ച അടിസ്ഥാനങ്ങളെ കുറിച്ചുള്ള സമീപനത്തിൽ നിന്നും വ്യത്യസ്തമായി ജ്യാമിതിയുടെ പ്രശ്‌നവൽക്കൃതമായ സങ്കല്പനങ്ങളിലാണ് ഡല്യൂസിന്റെ സമീപനം നിൽക്കുന്നത്. സത്താവാദത്തിന്റെ ദാർശനിക നിലപാടിനെ പിന്തുടരുന്ന സ്വയംസിദ്ധപ്രമാണങ്ങളുടെ ഗണിതശാസ്ത്രപദ്ധതിക്കു പകരം അതിൽ നിന്നും വിടുതൽ നേടുന്ന ഒരു ബദൽ പദ്ധതിയെ ഡല്യൂസ് സ്ഥാപിക്കാൻ ശ്രമിക്കുന്നു. നിർദ്ധാരണങ്ങൾ ഭാഷേതരമാണോ ഭാഷയിലൂടെ രേഖപ്പെടുന്നതാണോ എന്നീ പ്രശ്‌നങ്ങൾക്കപ്പുറത്ത് ഉത്തരങ്ങളെ ചോദ്യങ്ങൾക്കു കീഴ്‌പ്പെടുത്തുന്ന സമീപനമാണ് ഇവിടെ പ്രശ്‌നവൽക്കരിക്കപ്പെടുന്നത്. ചോദ്യങ്ങളേയും ഉത്തരങ്ങളേയും കുറിച്ചുള്ള പരമ്പരാഗതസമീപനത്തെ തിരിച്ചിടുകയാണ്.

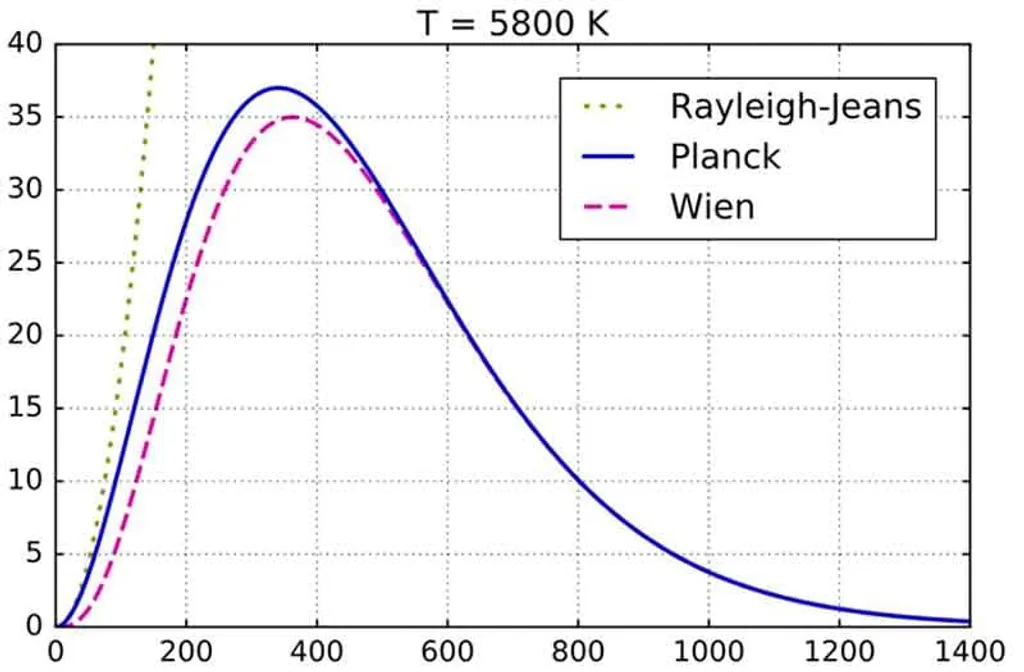
ഉത്തരങ്ങളിൽ നിന്നും ആരംഭിച്ച് നമുക്ക് ചോദ്യങ്ങളിലെത്തിച്ചേരാൻ കഴിയുമോ? നമ്മുടെ ഇപ്പോഴത്തെ ചിന്താരീതികളെ മറിച്ചിടുന്ന, മുൻഗണനാക്രമങ്ങളെ തിരിച്ചിടുന്ന ഒരു രീതി സാധ്യമാണോ? ശാസ്ത്രത്തിന്റെ ചരിത്രത്തിൽ നിന്നും ലളിതമായ ഒരു ഉദാഹരണം പറയാം. മാക്‌സ് പ്ലാങ്കിന്റെ ക്വാണ്ടം സങ്കൽപ്പനങ്ങൾ രൂപം കൊള്ളുന്നതു തന്നെ അങ്ങനെയാണ്. കറുത്ത പ്രതലങ്ങളിൽ നിന്നുള്ള വികിരണങ്ങളെ കുറിച്ചുള്ള വർണ്ണരാജിയെ വിശദീകരിക്കുന്നതിന് റാലേ-ജീൺ സിദ്ധാന്തവും വീൻ സിദ്ധാന്തവും പരാജയപ്പെടുന്നു. ഊർജ്ജപ്രവാഹത്തിന്റെ തുടർച്ചകളെ കുറിച്ചു പറയുന്ന ക്ലാസിക്കൽ സങ്കൽപ്പനങ്ങളിലാണ് ഇവ നിലയുറപ്പിച്ചിരുന്നത്. പ്രകൃതി കാണിക്കുന്ന വികിരണ വർണ്ണരാജി നിരീക്ഷണങ്ങളിലൂടെ ലഭ്യമായിരുന്നു. റാലേയും ജീനും ചേർന്നു രൂപീകരിച്ച സമീകരണം നൽകുന്ന വർണ്ണരാജി ഉയർന്ന ആവൃത്തികളിൽ പ്രകൃതിചിത്രത്തോട് യോജിക്കുന്നുണ്ടായിരുന്നില്ല. ഉയർന്ന ആവൃത്തികളിൽ ഊർജ്ജസാന്ദ്രത അനന്തമായി മാറുന്ന ദുരന്തത്തെയാണ് അത് പ്രവചിച്ചത്. വീനിന്റെ നിയമമാകട്ടെ, താഴ്ന്ന ആവൃത്തികളിലും പ്രവർത്തനക്ഷമമായിരുന്നില്ല. പ്രകൃതിചിത്രത്തിനു യോജിക്കുന്ന ഒരു ഗണിതശാസ്ത്രസമീകരണം എഴുതുകയാണ് മാക്‌സ് പ്ലാങ്ക് ചെയ്തത്. വർണ്ണരാജിയെ വിശദീകരിക്കാൻ കഴിയുന്ന സ്വയംസിദ്ധപ്രമാണങ്ങളെയോ അടിസ്ഥാനസങ്കൽപ്പനങ്ങളെയോ അന്വേഷിക്കുന്നതിനു പകരം ഗണിതശാസ്ത്രത്തിൽ വിശ്വാസമർപ്പിക്കുകയും പ്രയോഗങ്ങളിലുടെയും പരീക്ഷണങ്ങളിലൂടെയും അനുഭവങ്ങളിലൂടെയും ശാസ്ത്രജ്ഞന്മാർ സ്വായത്തമാക്കിയിരുന്ന പ്രകൃതിചിത്രത്തെ ഗണിതവൽക്കരിക്കുകയുമാണ് പ്ലാങ്ക് ചെയ്തത്. തനിക്കു ലഭിച്ച ഗണിതശാസ്ത്രസമീകരണം, അഥവാ പ്രകൃതിചിത്രത്തിന്റെ ഗണിതവിവർത്തനം ശരിയാകണമെങ്കിൽ, ഊർജ്ജത്തിന്റെ പ്രവാഹവും ഉത്സർജ്ജനവും ആഗിരണവുമെല്ലാം തുടർച്ചയുള്ള പ്രക്രിയകളാകണമെന്ന സങ്കൽപ്പനത്തെ ഉപേക്ഷിക്കണമെന്നും അവ ഇടർച്ചയുള്ള പ്രക്രിയകളാണെന്ന് സങ്കൽപ്പിക്കണമെന്നും പ്ലാങ്ക് കണ്ടെത്തുന്നു. ക്വാണ്ടം സിദ്ധാന്തം ഇങ്ങനെയാണ് ഉദ്ഘാടനം ചെയ്യപ്പെട്ടത്. മാക്‌സ് പ്ലാങ്കിന്റെ പ്രവർത്തനത്തെ തോമസ് കുൺ പകുതി പരിഹാസത്തോടെയാണ് (curve fitting formula)കണ്ടതെങ്കിലും ഡല്യൂസിന്റെ ദർശനത്തിന്റെ അടിസ്ഥാനത്തിൽ പ്ലാങ്കിന്റെ രീതിശാസ്ത്രത്തിന്റെ പ്രാധാന്യം വെളിവാകുന്നുണ്ട്. പ്രയോഗങ്ങളിൽ നിന്നും ആരംഭിക്കുക, ഗണിതവൽക്കരിക്കുക, സങ്കൽപ്പനങ്ങളേയും സംപ്രത്യയങ്ങളേയും രൂപീകരിക്കുക. ശാസ്ത്രത്തിന് ഇങ്ങനെയൊരു പ്രവർത്തനരീതിശാസ്ത്രം സാധ്യമാണ്. അത് വസ്തുനിഷ്ഠതയെ എത്തിപ്പിടിക്കുന്നതിന് സഹായകമാണ്.

ശാസ്ത്രവും ദർശനവും കലയും സാഹിത്യവുമെല്ലാം കൂടിച്ചേരുന്ന ഇടങ്ങളെ ഡല്യൂസ് കാണുന്നുണ്ട്. ഇവയോരോന്നിനും വ്യത്യസ്ത രീതികളുള്ളപ്പോഴും ഇവയുടെ കഴിവുകൾ കൂടിച്ചേരുകയും പരസ്പരം പ്രതിപ്രവർത്തിക്കുകയും ചെയ്യുന്നത് ആവശ്യമായിരിക്കുന്നുവെന്ന് ഡല്യൂസ് കാണുന്നുണ്ട്. ഇത് ധനാത്മകമായ കാര്യങ്ങളെ നിർവ്വഹിക്കുന്നതിന് ഉതകുന്നതാണ്. തത്വചിന്തയിലെ സംപ്രത്യയങ്ങളുടെ രൂപീകരണത്തെ സഹായിക്കുന്നതിനു ശാസ്ത്രചിന്തയ്ക്കു കഴിഞ്ഞേക്കാം. തത്ത്വചിന്തയിലെ സംപ്രത്യയങ്ങൾ ശാസ്ത്രത്തിന്റെ പ്രവർത്തനത്തേയും രീതിശാസ്ത്രത്തേയും വിശദീകരിക്കുന്നതിനു സഹായകമായേക്കാം. ലോകത്തെ സ്ഥിതമായി കാണുന്ന പ്രവണതകളെ അലോസരപ്പെടുത്തുകയും നിഷേധിക്കുകയും ചെയ്യുന്ന ബഹുലതകളുടെ (multiplicities) ലോകങ്ങളെ ഡല്യൂസ് കണ്ടെത്തുന്നു. ബഹുലതകളെ കുറിച്ച് സർഗപരമായ ഭവശാസ്ത്രം നിർമ്മിക്കുന്ന ഡല്യൂസ് തന്റെ പ്രവർത്തനങ്ങളിൽ ശാസ്ത്രത്തിന് പ്രധാനസ്ഥാനം നല്കി അനുയോജീകരിക്കുന്നുമുണ്ട്.

ശാസ്ത്രത്തിലെ ആശയങ്ങൾ തത്ത്വചിന്തയുടെ ദൗത്യവുമായി അനുനാദത്തിലാകുകയും നമ്മുടെ സ്ഥിതവും സാധാരണവും വ്യവസ്ഥാപിതവുമായ ചിന്താരീതികളെ അലോസരപ്പെടുത്തുകയും ചെയ്യും. ക്വാണ്ടം ബലക്ഷേത്രസിദ്ധാന്തങ്ങളിൽ ഉപയോഗിക്കുന്ന വിർച്ച്വൽ എന്ന ആശയത്തെ ഡല്യൂസ് സ്വീകരിക്കുന്നത് ഇങ്ങനെയാണെന്ന് നാം പറഞ്ഞു. ഗണിതശാസ്ത്രത്തിലെ റിമാനിയൻ സ്ഥലസങ്കല്പനങ്ങളെ ചലച്ചിത്രത്തിന്റെ വ്യാഖ്യാനത്തിന് അദ്ദേഹം ഉപയോഗിക്കുന്നത് ശാസ്ത്രത്തിലെ ചിന്തയെ കലയിൽ ഉപയോഗിക്കുന്നതിന്റെ ഉദാഹരണമാണ്. യൂക്ലിഡിയൻ സ്ഥലസങ്കല്പനങ്ങൾക്കും അരിസ്റ്റോട്ടിലിന്റെ കാലസങ്കല്പനങ്ങൾക്കും ന്യൂട്ടന്റെ ഭൗതികശാസ്ത്രത്തിനും സമാന്തരമായി ഒരു ദാർശനികവ്യവസ്ഥയെ കാന്റ് രൂപപ്പെടുത്തിയതു പോലെ നേർരേഖീയമല്ലാത്ത ബലതന്ത്രത്തിനും തുടർച്ചാരഹിതവും ശകലീകരിക്കപ്പെട്ടതുമായ സ്ഥലസങ്കല്പനങ്ങൾക്കും മടക്കിയെടുക്കാവുന്ന കാലത്തിനും യോജിച്ച ഒരു ദാർശനികവ്യവസ്ഥയെ സൃഷ്ടിക്കുകയാണ് ഡല്യൂസ് ചെയ്തതെന്നു കരുതുന്നവരുണ്ട്. അദ്ദേഹം പുതിയ ഭൗതികവാദത്തിനു രൂപം നല്കുകയായിരുന്നുവത്രെ! ദ്രവ്യത്തെ പിണ്ഡമെന്നു കരുതുന്നതിനേക്കാൾ നല്ലത് ഊർജ്ജമെന്നു കരുതുന്നതാണെന്ന് വിചാരിക്കുന്ന ഈ ചിന്തകൻ, ഈ വീക്ഷണത്തിലൂടെ ദ്രവ്യത്തിന്റെ സർഗശേഷികളിൽ ഊന്നുന്നു. ദ്രവ്യം തുടർച്ചയായ മാറ്റത്തിന്റേയും വ്യതിചലനങ്ങളുടേയും അവസ്ഥയിലാണെന്നതിലാണ് ഡല്യൂസിന്റെ ഊന്നൽ.
ലോകവുമായുള്ള നമ്മുടെ ബന്ധം ചലനാത്മകമാണ്. ലോകം നിരന്തരം മാറിക്കൊണ്ടിരിക്കുന്നതു കൊണ്ടു മാത്രമല്ല, ലോകത്തെ കുറിച്ചുള്ള നമ്മുടെ ആശയങ്ങൾ മാറിക്കൊണ്ടിരിക്കുന്നുവെന്നതു കൊണ്ടു മാത്രമല്ല, ജീവിതം തന്നെയും നിരന്തരം മാറുകയും പുനഃസൃഷ്ടിക്കപ്പെടുകയും ചെയ്തു കൊണ്ടിരിക്കുകയാണ്. സ്ഥിതമായിരിക്കുന്ന എന്തിന്റെയോ മാറിത്തീരലായിട്ടാണ് ഇതിനെ നാം കാണുന്നത്. ഇത് ശരിയല്ല. ഇതിനെതിരെ ഡല്യൂസ് ചിന്തിക്കുന്നു- നാം ചലനത്തിൽ നിന്നാണ് ആരംഭിക്കുന്നത്. മാറുകയും ആയിത്തീരുകയും ചെയ്യുന്ന പ്രവണതകളെയാണ് നാം അഭിമുഖീകരിക്കുന്നത്. ആയിത്തീരലിന്റെ ചലനതലമായി നാം ലോകത്തെ കാണുന്നു. പ്രതിനിധാനം ചെയ്യപ്പെടേണ്ട വസ്തുവായി, വിഷയമായി നാം ലോകത്തെ കാണുന്നില്ല. നമ്മുടെ ചിന്ത ലോകത്തെ പ്രതിനിധാനം ചെയ്യുന്നതാണെന്ന രീതിയിൽ, ലോകത്തിൽ നിന്നും മാറിനില്ക്കുന്ന മറ്റൊന്നായി നാം കാണുന്നില്ല. ചിന്ത ലോകത്തിന്റെ ചലനത്തിന്റേയും ഒഴുക്കിന്റേയും ഭാഗമാണ്. ചിന്തിക്കുകയെന്നാൽ ജീവിതത്തെ പ്രതിനിധാനം ചെയ്യുകയെന്നല്ല, ജീവിതത്തിൽ പ്രവർത്തിക്കുകയും പരിവർത്തിപ്പിക്കുകയുമെന്നാണ്. അതീതത്തിനെതിരെ അന്തർലീനതയെ മുന്നോട്ടു വയ്ക്കുകയാണ് ഡല്യൂസ് ചെയ്യുന്നത്. അതീതം ബാഹ്യമായിട്ടുള്ളതിനെ കുറിച്ചു പറയുന്നു. എന്നാൽ, അന്തർലീനമായിരിക്കുന്നതിൽ ബാഹ്യമായ മറ്റൊന്നുമില്ല. അതീതത്തെ കുറിച്ചു പറയാതെ, ദൈവത്തെ കുറിച്ചു പറയാതെ ഡല്യൂസ് ജീവിതത്തിന്റെ അന്തർലീനതയെ കുറിച്ചു പറയുന്നു.▮

​​​​​​​(തുടരും)